Agrupamento Geográfico Com Um Algoritmo Evolutivo
Nesta página... (^^)
Campeonato de Portugal 2019/20 - distâncias entre equipas
O Campeonato de Portugal de futebol de 11 masculino da época 2019/20 contou com 72 equipas divididas em 4 séries. Como é tradicional no futebol Português as séries foram divididas em faixas de norte para sul. Sendo Portugal continental aproximadamente retangular esta é uma forma simples de obter faixas de território tais que as equipas estejam próximas entre si. As equipas das Regiões Autónomas (3 dos Açores, 3 da Madeira) são incluídas em conjunto numa das séries a norte (as da Madeira) e numa das séries a sul (as dos Açores).
As questões que aqui coloco são, primeiro, será possível uma organização diferente das séries que minimize a distância percorrida pela totalidade das equipas? Dada a simplicidade da atual forma de formar as séries é de esperar que sim. Segundo, e principalmente, de quanto será esse ganho? A questão de interesse prático é uma terceira: merece a pena implementar tal método? Essa no entanto carece de muito mais informação para ser respondida, além de que em última análise a definição de quais os critérios que melhor servem os seus interesses e necessidades será sempre uma opção política da organização.
O interesse é de ter noção da ordem de grandeza do ganho, pelo que para cada equipa vamos usar a localização do seu estádio e medir distâncias percorridas como distâncias "em voo de pássaro" entre estádios. Isto simplifica bastante a recolha de dados, pois bastam as 72 localizações e usar uma função para determinar as distâncias. Para ter distâncias rodoviárias, reais, seria necessário determinar mais de 5 mil trajetos entre cada par de equipas e em cada sentido. Igualmente por simplicidade as equipas dos Açores e da Madeira são consideradas como localizadas nos aeroportos de Lisboa e Porto, respetivamente, em linha com a distribuição oficial.
Talvez seja possível criar um algoritmo exato para determinar a solução ótima. Visto que estamos a procurar apenas uma boa aproximação de forma rápida vamos usar um método genérico, um algoritmo genético, para determinar a solução. Por isso, e porque eu estava com vontade de implementar um em Octave para treinar a linguagem e refrescar o algoritmo. Tem a vantagem de ser relativamente simples de implementar, mas a desvantagem de poder chegar a uma solução que não é a ótima. Neste caso, sendo o problema pequeno, foi possível correr o algoritmo diversas vezes tendo chegado sempre ao mesmo resultado. Também foram verificadas manualmente algumas alternativas que não pareciam muito distantes, mas nenhuma era melhor.
Resumo dos resultados
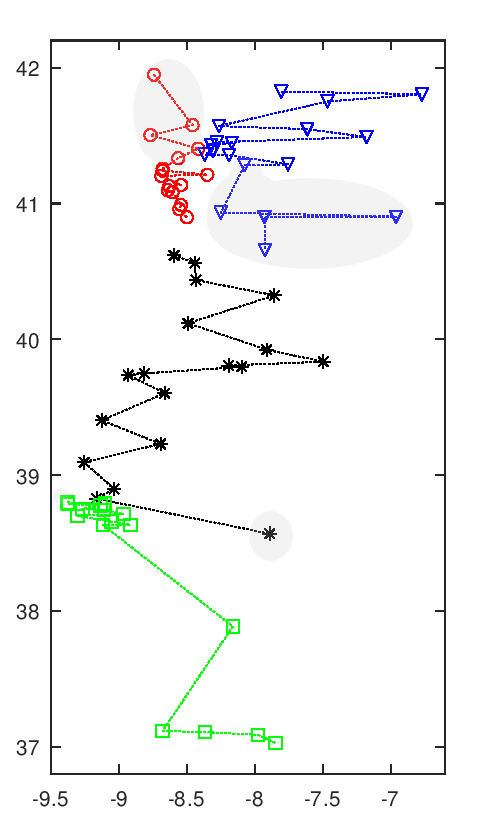
Séries por Proximidade (a cinza as equipas que trocam)1
As duas séries da zona norte do país originais e "de proximidade" são quase ortogonais. A organização por proximidade resultante numa série junto ao litoral e outra no interior, com uma linha de separação quase vertical ao invés da linha horizontal oficial. Entre as duas séries a centro e sul do país apenas duas equipas a trocarem de série. O Lusitano de Évora, apesar de ser a sexta equipa mais a sul,2 fica colocado na zona "centro", por troca com o Sintrense.3
Para ter uma comparação correta consideram-se não as séries oficiais, mas as séries que se obteriam com uma estrita divisão em faixas de norte para sul. Neste caso as equipas das Regiões Autónomas ficariam noutras séries por troca com três outras equipas. Nessa organização, as equipas viajariam um total de 105,237 km. Na organização resultante desta minimização das distâncias a distância total a viajar reduz-se para 99,598 km. Um ganho total de 5,639 km. Isto representa um ganho médio de 78 km por equipa, ou ainda de 4.6 km por equipa e por viagem. O ganho relativo entre estes valores é de 5.4%, mas o ganho relativo real será menor, pois não estamos a considerar as deslocações nos Açores e Madeira (por serem uma constante, não interferem na minimização).
As variações individuais, em termos relativos, são por vezes bastante distantes destes 5%. Num extremo Trofense, com redução de 59% da distância (de 1,183.6 km para 487.1 km) e Sp. Braga 'B' com 48% (de 1,457.4 km para 753.8 km). No outro Arouca com um aumento de 59% da distância (de 867.0 km para 1,382.4 km) e Maria da Fonte com um aumento de 27% (de 907.7 km para 1,155.1 km). Em termos absolutos as maiores variações seriam do Sintrense com redução de 1,036.5 km (de 2,470.5 km para 1,434.0 km) e do já referido Sp. Braga 'B' com redução de 703.6 km. Os maiores aumentos absolutos seriam de Arouca com 515.4 km e do Lusitano de Évora com aumento de 391.1 km (de 2443.0 km para 2834.1 km). É de notar que a correlação entre ganhos de distância com a distância inicial é de zero (r=-0.003).4
Pode ver resultados mais detalhados no final, em apêndice.
Será interessante rever esta forma de arrumação num caso com mais equipas e mais grupos, onde será de esperar séries ainda menos organizadas de norte para sul, pois a restrição imposta pela forma relativamente estreita do território torna-se menos relevante.
Uma visão geral sobre algoritmos evolutivos
Os algoritmos evolutivos são uma classe de métodos de optimização inspirados em genética e evolução por seleção natural. Supomos que as soluções são como "seres vivos". Os seres vivos são gerados a partir da codificação existente num "DNA". O DNA é uma sequência de "genes". Os genes são instruções relativamente simples. Os seres vivos mais aptos terão maior probabilidade de se reproduzirem, gerando novos seres que têm material genético que é uma mistura do dos progenitores. Finalmente, presume-se que podem existir mutações no DNA.
Vejamos então como aplicar num programa os conceitos de Codificação, Aptidão, Seleção, Cruzamento e Mutação. Primeiro genericamente, depois aplicando ao nosso problema.
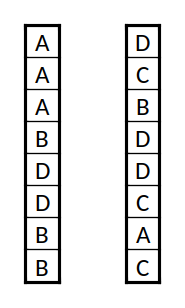
Duas "cadeias de DNA", com os "genes" 'A', 'B', 'C', e 'D'
A codificação tem duas componentes: os "genes" e a "cadeia de ADN". A cadeia de ADN será simplesmente uma lista ordenada dos genes. O objetivo ao usar listas é de ter grande flexibilidade. Numa lista pode-se trocar a ordem, alterar, acrescentar, ou retirar elementos. Entre listas pode-se trocar elementos. Os genes são a parte da codificação mais específica do problema. Têm de ser tais que uma sequência deles gere soluções. Por exemplo, se estivermos a criar uma imagem cada gene pode conter informação sobre que cor usar, em que local da imagem, com que tipo de traço, e assim sucessivamente; se estivermos a criar um objecto pode ser que tipo de peça usar, ligada a qual das anteriores, em que posição, de que forma se move, etc.. Note-se que o espaço de soluções gerado por esta codificação pode ter uma quantidade enorme de soluções (provavelmente) distintas. Se algum dos parâmetros que definem os genes forem contínuos, então o espaço de soluções é em teoria infinito, sendo apenas limitado de facto pela capacidade de representação interna das variáveis na linguagem de programação utilizada.
A aptidão mais simples é obtida por uma função que associe cada codificação a um valor real, sendo que maior é melhor. Pode não ser nada evidente como criar tal função, por exemplo se estiver a criar criaturas tridimensionais capazes de se deslocar, ou nadar, ou combater pela posse de um objeto5 será necessário fazer simulações e medir distâncias ou quantidade de vitórias. De uma forma ou de outra a aptidão pode não ser determinística (e mesmo sendo determinística, pode ser caótica).
A seleção consiste em escolher mais vezes as soluções mais aptas para gerarem descendentes. Por exemplo escolhendo um subconjunto aleatório de soluções e de entre essas selecionar a mais apta para "se reproduzir". Pode ser escolhendo a com aptidão mais alta, ou pode ser necessário fazer um torneio entre as candidatas para escolher uma. O efeito é de que as soluções mais aptas devem em geral gerar várias descendentes, enquanto as menos aptas vão gerar poucas ou nenhumas.
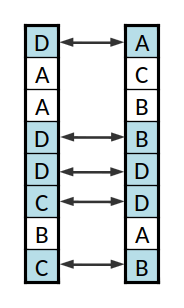
Um cruzamento das cadeias de ADN anteriores
O cruzamento consiste em misturar as duas listas. O caso mais simples será de escolher uma posição nas listas aleatoriamente e trocar a a sub-lista a partir dessa posição. Uma alternativa mais sofisticada, e que evita correlações diferentes entre genes que podem ser indesejadas, consiste em percorrer as listas e para cada par de genes trocar ou não com uma dada probabilidade. Neste caso de cada dois progenitores obtém-se dois descendentes, mas pode-se usar apenas um (por exemplo por sorteio).
A mutação consiste em fazer alguma alteração, aleatória, na cadeia de ADN seja mudando genes de posição (por exemplo trocado dois a dois) ou alterando parâmetros de algum(s) gene(s).
Implementação
A implementação básica de um algoritmo genético, consiste em:
- Criar uma população inicial
- Repetir, até ter uma nova população do tamanho da população inicial:
- Escolhe dois progenitores
- Gera dois descendentes
- Muta os descendentes
- Coloca os descendentes na nova população
- Caso a melhor solução seja suficientemente boa, ou se tenha esgotado o tempo:
- Termina
- Caso continue:
- Substitui a população inicial pela nova população
- Repete a partir de 2.
Ao longo de todo o processo, ir tomando nota de qual a melhor solução encontrada até ao momento.
Sobre este esquema base as variações possíveis são imensas. O principal compromisso é entre explorar regiões diferentes do espaço de soluções, ou aperfeiçoar as melhores soluções encontradas.6 Uma escolha de progenitores muito seletiva (por exemplo torneios com sete, dez, ou mais candidatos) foca a solução no aperfeiçoamento das melhores soluções atuais. Mutações frequentes ou grandes permitem explorar novas soluções. Pode-se fazer as soluções mais aptas passar de uma geração para a outra, para concentrar em aperfeiçoar essas. Pode mesmo ser útil variar os parâmetros ao longo do cálculo, por exemplo reduzindo o nível de mutação, para ir passando de uma fase inicial de exploração para uma seguinte de aperfeiçoamento.
A flexibilidade é imensa, e penso que ainda tem tanto de arte, com ajustes caso a caso, quanto de ciência, pois o comportamento do algoritmo em si ainda é objeto de estudo teórico. Convém que uma implementação registe dados intermédio que permitam analisar a evolução das soluções e testar várias configurações.
Notas sobre o algoritmo implementado
O problema em concreto, de determinar os grupos por proximidade geográfica é de esperar que seja "bem comportado", ou seja que seja possível ir melhorando as soluções através de pequenos ajustes sucessivos das soluções. A quantidade de grupos diferentes 18 equipas formados a partir de 72 equipas é imenso, da ordem7 de {$6 \times 10^{37}$}.
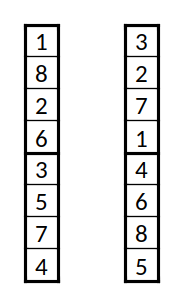
Duas instâncias da codificação usada, em versão reduzida (8 equipas, 2 grupos)
Para a codificação, associa-se a cada equipa um índice de 1 a 72, e a codificação consiste numa lista com uma permutação dos inteiros de 1 a 72. Os grupos são definidos fazendo quatro partições iguais da lista (ou seja, os primeiros 18 elementos serão o primeiro grupo, e assim sucessivamente). Um exemplo para um caso reduzido com 8 equipas e 2 grupos é a lista {$\lbrace 1,8,2,6,3,5,7,4 \rbrace$}, que indica que os primeiro grupo é formado pelas equipas 1, 8, 2, e 6; e o segundo grupo pelas 3, 5, 7, e 4.
A maioria da implementação não foge das linhas gerais dadas acima. A população é grande, umas centenas de soluções, para permitir alguma exploração inicial, mas presume-se que irá convergindo de forma estável para soluções melhores. A aptidão é a grandeza que se quer minimizar, a distância total percorrida pelas equipas. A mutação é pouco agressiva, fazendo uma média de 2 trocas de posição de índices (quantidade de trocas com distribuição de Poisson, pelos que em muitos casos haverá apenas uma ou mesmo nenhuma troca, mas poderá chegar à dezena, raramente). Os progenitores são selecionados como o melhor de dois.
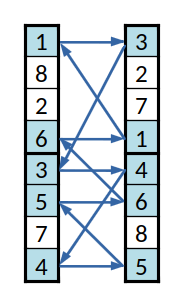
Primeiro conjunto cíclico
O aspeto mais interessante será o cruzamento, que não pode ser tão simples quanto apenas trocar elementos entre as listas. No caso do par de listas da imagem, se se trocasse os primeiros elementos ( o 1, com o 3), a primeira lista ficaria com dois índices 3, o que não é uma solução válida, pois indicaria que uma dada equipa, a (3), estava em dois grupos diferente e que a equipa (1) não estava em nenhum.
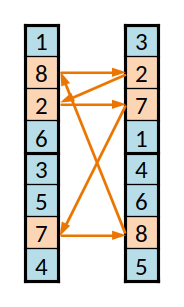
Segundo conjunto cíclico
Para evitar esse problema criam-se "conjuntos cíclicos" de equipas. Seguindo o exemplo dado, para trocar a (1) com a (3) e para manter a codificação válida, é necessário trocar também a (3), neste caso pela (4); pelo mesmo motivo é então necessário trocar a (4) por outra, e assim sucessivamente até o ciclo se fechar, regressando à equipa (1).
Procede-se assim para os genes seguintes. Na implementação feita trocou-se exatamente um em cada dois destes conjuntos, mas seria provavelmente melhor troca-se ou não com uma dada probabilidade.
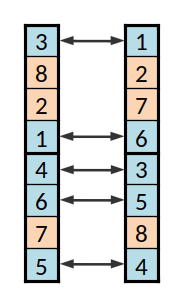
Os dois descendentes, cruzando o primeiro conjunto
Evolução!
A imagem seguinte tem uma animação com todas as soluções intermédias de uma execução do algoritmo.
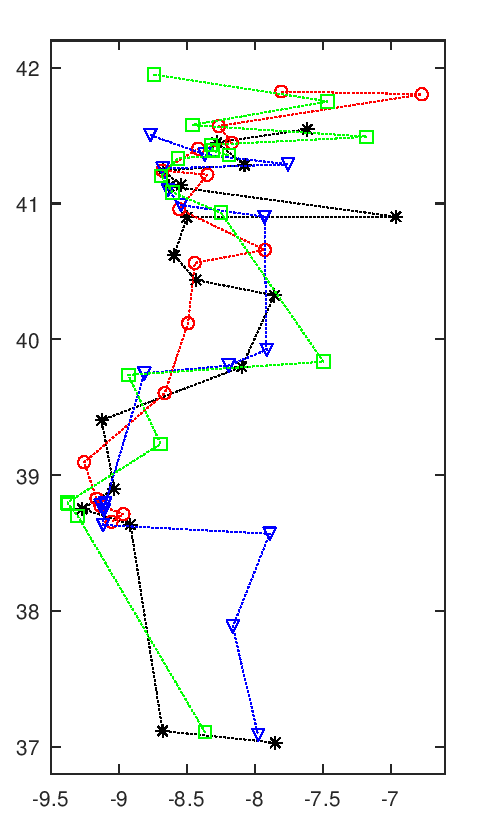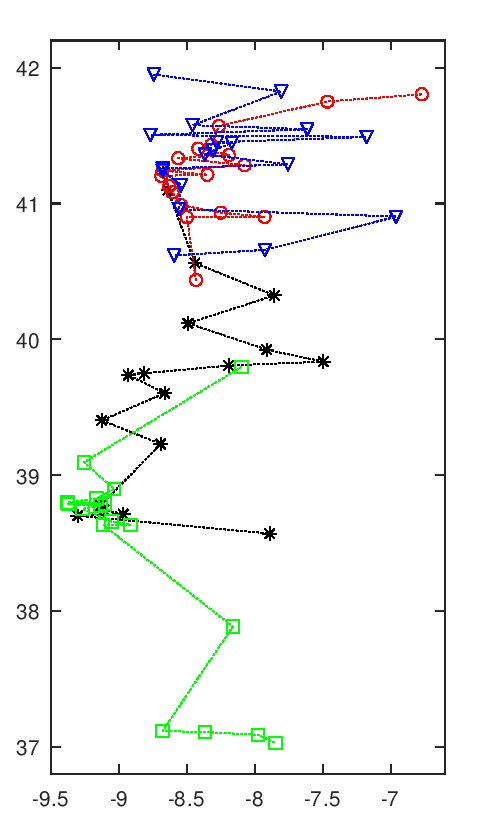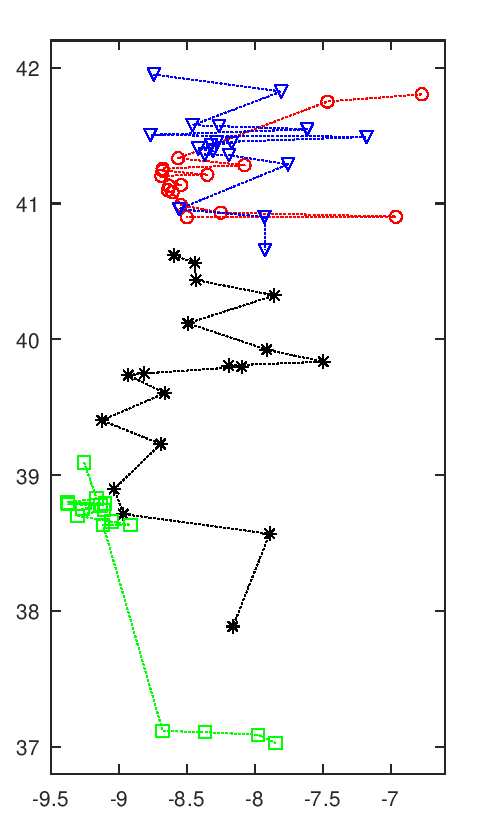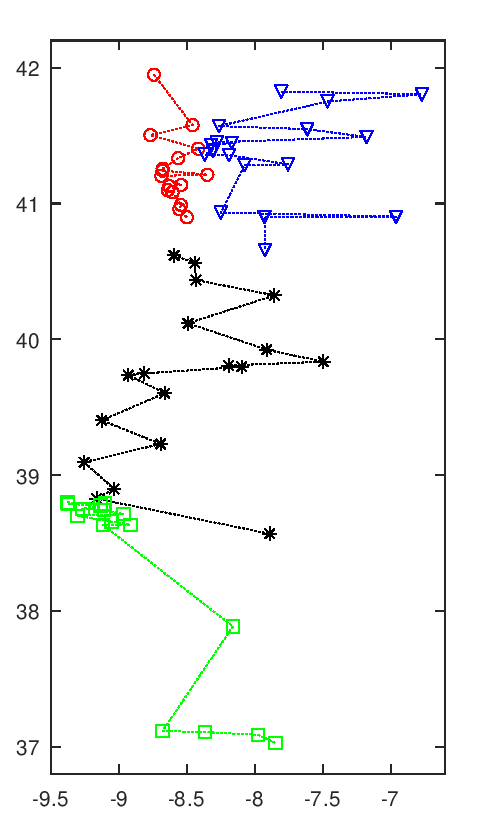
Evolução da melhor solução
Nota-se que as primeiras solução são muito más, o que é normal pois são completamente aleatórias. Rapidamente se vão formando núcleos de equipas, que claramente são melhores soluções. Depois demora a chegar a uma solução final, apenas com ajustes que são aleatórios. Esta evolução a partir de meio parece notar-se a existência de duas "estirpes" de soluções que vão alternando em melhorias sucessivas paralelas, p.ex. nota-se o Rec. de Águeda (40.6 N, 8.4 O) a alternar entre o norte litoral, a vermelho, e o centro, a preto.
Esta animação mostra as soluções a intervalos certos, na realidade pode haver fases de paragem seguidas de fases com várias evoluções em rápida sucessão. Essa é uma interessante característica deste algoritmo, parece bloquear-desbloquear e dar saltos bruscos.
Anexo e leituras
- prt3-2021.m, a implementação em Octave usada para a elaboração deste texto.
- Luke, Sean, "Essentials of Metaheuristics", v2.2 (2015), https://cs.gmu.edu/~sean/book/metaheuristics/ (gmu.edu - George Mason University), com algoritmos genéticos, e muito mais, de um ponto de vista prático , de longe a principal fonte deste texto. PDF de acesso livre, o autor pede para preencher um pequeno formulário, pode preencher que de facto ele não abusa do endereço de email.
- Mitchell, Melanie, "An Introduction to Genetic Algorithms" (1999), p.ex. em https://www.semanticscholar.org/paper/An-introduction-to-genetic-algorithms-Mitchell/03cb4e2cb669d3f6344a733e622f07909f87ff0a. Confesso que este apenas li na diagonal. Tem estudo dos fundamentos teóricos do algoritmo genético, que espero ler com mais cuidado um dia.
Apêndice
As séries por proximidade
As séries por proximidade seriam as seguintes, indicando-se as alterações em relação a séries norte-sul.
| A (norte interior) | B (norte litoral) | C (centro) | D (sul) |
|---|---|---|---|
| Montalegre | (*) Cerveira | Beira-Mar | (+) Sintrense |
| Bragança | (*) Merelinense | Rec. Águeda | Sacavenense |
| Chaves Satélite | (*) Sp. Braga B | Anadia | 1º Dezembro |
| Maria da Fonte | (*) Oliveirense | Oliv. Hospital | Fontinhas |
| Juv. Pedras Salgadas | (*) Trofense | Condeixa | Ideal |
| Mirandela | Pedras Rubras | Oleiros | Praiense |
| Vit. Guimarães B | Câmara de Lobos | Benfica Castelo Branco | Real |
| Fafe | Marítimo B | Vit. Sernache | Oriental |
| Berço | Un. Madeira | Sertanense | Olímpico Montijo |
| Vizela | Paredes | Un. Leiria | Sintra Football |
| São Martinho | Leça | Marinhense | Fabril Barreiro |
| Felgueiras 1932 | Gondomar | Fátima | Pinhalnovense |
| Vila Real | Coimbrões | Caldas | Amora |
| (*) Amarante | Valadares Gaia | Un. Santarém | Aljustrelense |
| (*) Arouca | Canelas 2010 | Torreense | Esp. Lagos |
| (*) Gin. Figueirense (C.Rodrigo) | Lusitânia de Lourosa | Alverca | Armacenenses |
| (*) Castro Daire | Sp. Espinho | Loures | Louletano |
| (*) Lusitano Vildemoinhos | Sanjoanense | (+) Lusit. Évora | Olhanense |
| A (norte interior) | B (norte litoral) | C (centro) | D (sul) |
legenda
| (*) | equipa com série diferente (trocas {$A \leftrightarrow B$}) |
| (+) | equipa com série diferente (troca {$C \leftrightarrow D$}) |
Alterações de distância e série
Todas as equipas, de norte para sul. Indicam-se as séries oficiais, estritamente norte-sul, e por proximidade; tal como o ganho de sistâncias e as distâncias totais para as séries norte-sul e por proximidade.
| {$S_0$} | {$S_1$} | {$S_2$} | equipa | {$\Delta D_{12}$} | {$D_1$} | {$D_2$} |
|---|---|---|---|---|---|---|
| A | A | B | Cerveira (*) | 264.7 | 1703.7 | 1439.0 |
| A | A | A | Montalegre | -69.0 | 1285.6 | 1354.6 |
| A | A | A | Bragança | 237.3 | 2706.9 | 2469.6 |
| A | A | A | Chaves Satélite | 89.1 | 1572.7 | 1483.6 |
| A | A | B | Merelinense (*) | 203.9 | 1031.3 | 827.4 |
| A | A | A | Maria da Fonte | -247.5 | 907.7 | 1155.1 |
| A | A | A | Juv. Pedras Salgadas | 113.1 | 1323.1 | 1210.0 |
| A | A | B | Sp. Braga B (*) | 703.6 | 1457.4 | 753.8 |
| A | A | A | Mirandela | 259.2 | 1947.8 | 1688.6 |
| A | A | A | Vit. Guimarães B | -207.7 | 865.8 | 1073.6 |
| A | A | A | Fafe | -122.2 | 884.5 | 1006.6 |
| A | A | A | Berço | -231.2 | 879.4 | 1110.6 |
| A | A | B | Oliveirense (*) | 305.1 | 960.4 | 655.3 |
| A | A | A | Vizela | -198.1 | 890.3 | 1088.3 |
| A | A | A | São Martinho | -229.9 | 942.9 | 1172.8 |
| B | A | A | Felgueiras 1932 | -86.5 | 916.1 | 1002.6 |
| B | A | B | Trofense (*) | 696.5 | 1183.6 | 487.1 |
| B | A | A | Vila Real | 176.3 | 1260.4 | 1084.1 |
| {$S_0$} | {$S_1$} | {$S_2$} | equipa | {$\Delta D_{12}$} | {$D_1$} | {$D_2$} |
| B | B | A | Amarante (*) | 102.4 | 1095.4 | 993.1 |
| B | B | B | Pedras Rubras | 323.8 | 755.7 | 431.9 |
| A | B | B | Câmara de Lobos (m) | 314.7 | 738.1 | 423.4 |
| A | B | B | Marítimo B (m) | 314.7 | 738.1 | 423.4 |
| A | B | B | Un. Madeira (m) | 314.7 | 738.1 | 423.4 |
| B | B | B | Paredes | 117.3 | 771.9 | 654.6 |
| B | B | B | Leça | 293.8 | 729.9 | 436.1 |
| B | B | B | Gondomar | 187.2 | 643.1 | 455.9 |
| B | B | B | Coimbrões | 224.1 | 661.2 | 437.0 |
| B | B | B | Valadares Gaia | 209.4 | 671.6 | 462.1 |
| B | B | B | Canelas 2010 | 184.2 | 653.9 | 469.6 |
| B | B | B | Lusitânia de Lourosa | 96.3 | 685.5 | 589.3 |
| B | B | B | Sp. Espinho | 86.7 | 714.1 | 627.4 |
| B | B | A | Arouca (*) | -515.4 | 867.0 | 1382.4 |
| B | B | A | Gin. Figueirense (C.Rodrigo) (*) | 677.1 | 2889.3 | 2212.1 |
| B | B | A | Castro Daire (*) | -60.1 | 1249.3 | 1309.4 |
| B | B | B | Sanjoanense | 24.1 | 772.1 | 748.1 |
| B | B | A | Lusitano Vildemoinhos (*) | -203.7 | 1447.1 | 1650.9 |
| {$S_0$} | {$S_1$} | {$S_2$} | equipa | {$\Delta D_{12}$} | {$D_1$} | {$D_2$} |
| C | C | C | Beira-Mar | -20.8 | 2069.9 | 2090.7 |
| C | C | C | Rec. Águeda | -8.0 | 1973.9 | 1982.0 |
| C | C | C | Anadia | -6.0 | 1809.8 | 1815.8 |
| C | C | C | Oliv. Hospital | 44.8 | 2117.2 | 2072.4 |
| C | C | C | Condeixa | -8.1 | 1511.2 | 1519.2 |
| C | C | C | Oleiros | 55.3 | 1802.0 | 1746.8 |
| C | C | C | Benfica Castelo Branco | 92.0 | 2424.4 | 2332.4 |
| C | C | C | Vit. Sernache | 31.6 | 1510.1 | 1478.5 |
| C | C | C | Sertanense | 42.5 | 1588.6 | 1546.1 |
| C | C | C | Un. Leiria | -43.8 | 1421.2 | 1465.1 |
| C | C | C | Marinhense | -58.8 | 1497.1 | 1555.8 |
| C | C | C | Fátima | -23.9 | 1390.8 | 1414.8 |
| C | C | C | Caldas | -93.5 | 1712.7 | 1806.2 |
| C | C | C | Un. Santarém | -25.5 | 1620.7 | 1646.2 |
| C | C | C | Torreense | -127.6 | 2022.9 | 2150.5 |
| D | C | C | Alverca | -92.9 | 2049.2 | 2142.1 |
| D | C | C | Loures | -120.9 | 2219.6 | 2340.5 |
| D | C | D | Sintrense (*) | 1036.5 | 2470.5 | 1434.0 |
| {$S_0$} | {$S_1$} | {$S_2$} | equipa | {$\Delta D_{12}$} | {$D_1$} | {$D_2$} |
| D | D | D | Sacavenense | 106.6 | 1306.1 | 1199.5 |
| D | D | D | 1º Dezembro | 165.8 | 1588.9 | 1423.2 |
| C | D | D | Fontinhas (a) | 113.4 | 1295.7 | 1182.3 |
| C | D | D | Ideal (a) | 113.4 | 1295.7 | 1182.3 |
| C | D | D | Praiense (a) | 113.4 | 1295.7 | 1182.3 |
| D | D | D | Real | 141.8 | 1413.7 | 1271.9 |
| D | D | D | Oriental | 106.7 | 1272.1 | 1165.4 |
| D | D | D | Olímpico Montijo | 74.4 | 1301.2 | 1226.8 |
| D | D | D | Sintra Football | 144.4 | 1440.2 | 1295.7 |
| D | D | D | Fabril Barreiro | 90.7 | 1258.1 | 1167.5 |
| D | D | D | Pinhalnovense | 59.8 | 1318.9 | 1259.1 |
| D | D | D | Amora | 102.4 | 1273.2 | 1170.9 |
| D | D | C | Lusit. Évora (*) | -391.1 | 2443.0 | 2834.1 |
| D | D | D | Aljustrelense | -87.4 | 2176.7 | 2264.1 |
| D | D | D | Esp. Lagos | -18.3 | 2708.9 | 2727.2 |
| D | D | D | Armacenenses | -48.1 | 2771.7 | 2819.8 |
| D | D | D | Louletano | -81.1 | 3057.7 | 3138.8 |
| D | D | D | Olhanense | -88.8 | 3266.5 | 3355.3 |
| {$S_0$} | {$S_1$} | {$S_2$} | equipa | {$\Delta D_{12}$} | {$D_1$} | {$D_2$} |
legenda
| {$S_0$} | séries oficiais |
| {$S_1$} | séries norte-sul |
| {$S_2$} | séries por proximidade |
| {$D_1$} | distância total, em série norte-sul |
| {$D_2$} | distância total, em série por proximidade |
| {$\Delta D_{12}$} | redução na distância total |
| (*) | equipa com série diferente |
| (a) | equipa da R.A. Açores |
| (m) | equipa da R.A. Madeira |
1 Os mapas são em função de latitude e longitude, portanto as distancias horizontais a norte estão algo exageradas em relação às a sul (uns 7% entre topo e fundo) tal como a largura está maior, em proporção que a altura (uns 30% no centro), lamento mas não tinha nenhuma projeção geográfica à mão, e fazer uma é todo um outro texto... ⇑
2 De facto é a nona mais a sul, mas nesta distribuição as três equipas da Madeira "estão" no aeroporto do Porto ⇑
3 Que no mapa é indistinguível do 1º de Dezembro ⇑
4 Interrogo-me se este zero (quase) exato será apenas uma interessante coincidência ou uma característica do problema. ⇑
5 Karl Sims - Evolved Virtual Creatures, Evolution Simulation, 1994, https://www.youtube.com/watch?v=JBgG_VSP7f8 ⇑
6 Em inglês: exploration vs exploitation. ⇑
7 salvo erro: {$\frac{1}{4!} \binom{4\times18-1}{17} \binom{3\times18-1}{17} \binom{2\times18-1}{17}$}, mas faça o leitor o favor de verificar e corrigir ou apontar uma expressão mais simples, que estas combinações podem ser traiçoeiras ⇑